ひっひっひ……今日はのう、「自然」とのつき合い方をデータで斬ってみせよう。
風が吹けばインが飛ぶ、波が立てば荒れる――耳にタコができるほど聞く話じゃが、本当のところはどうなのか。
2025年1月1日〜8月13日の全レースを材料に、風速・波高と配当(払戻金)、そして イン逃げ失敗 の関係をまとめ直したぞい。

風や波は舟券を揺さぶるのか?おばばが分析
📏 データと分析方法
- 期間:2025/01/01〜2025/08/13
- 指標:
- 払戻金 … 荒れ具合の目安。※桁ぶれを抑えるため 対数変換 で評価
- 風速(m/s)・波高(m)
- イン逃げ失敗
- 可視化:
- 散布図(風/波 × 対数払戻金):色の濃さ=頻度
- 折れ線図(風速/波高 × イン逃げ失敗率):左から右に行くほど環境条件が厳しい
💨 風速 × 払戻金
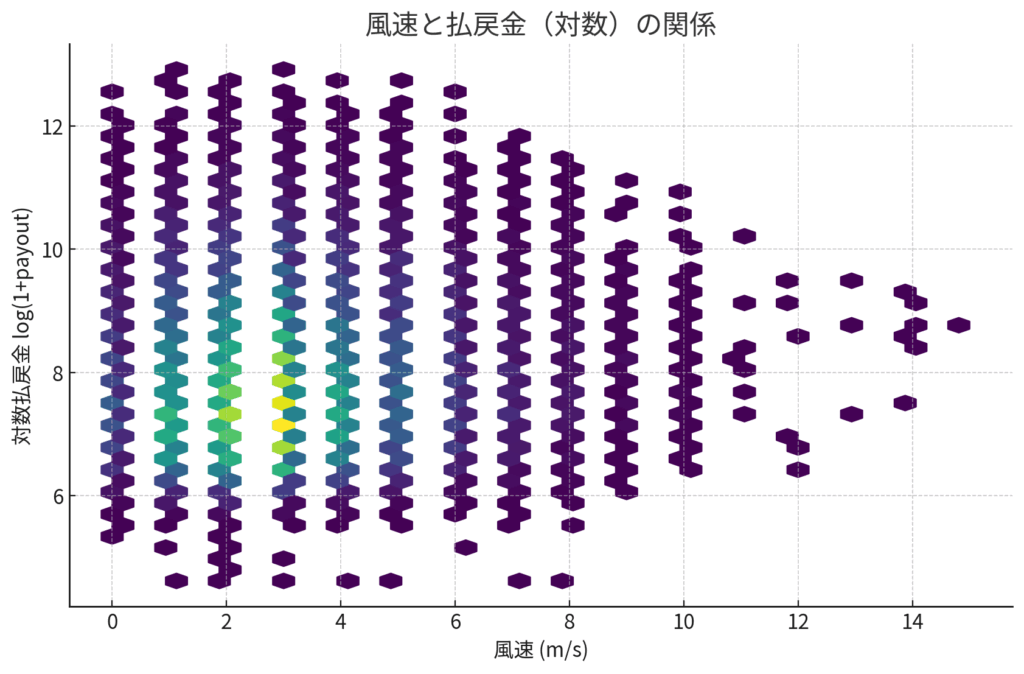
グラフの見方
- X軸:風速(m/s)
- Y軸:払戻金(対数変換、上に行くほど高配当)。なお、Y軸の目盛りはそれぞれ以下の払戻金に相当するぞい
- ln = 6 → 約 400円
- ln = 8 → 約 2,980円
- ln = 10 → 約 22,000円(万舟ゾーン)
- ln = 12 → 約 162,800円(10万舟ゾーン)
- 色:点の頻度を表す
- 緑〜黄色=頻度が高い典型的なゾーン
- 紫色=めったに起きないレアケース
- 相関があるなら、データの分布が斜め(右上がり/右下がり)に伸びる
分析
ひっひっひ、見てみい。緑や黄色の濃い帯は、弱風でも強風でも 横一列に低配当域に広がっとる。つまり大半のレースは「安めの決着」で収まっておるのじゃ。
一方、紫色の散発的な点は、風が弱いときにも強いときにも 縦に飛んどる。
つまり高配当は「風が強いから出る」のではなく、いつでも条件次第で発生する。
結論
風は舟券を揺らさない
風速と払戻金には相関がないことがわかったじゃろ。つまり、強風=荒れるとは限らんのじゃ。ただし強風時はレース展開が乱れやすく、堅い決着ばかりに収まらず、配当の幅も揺らぐ余地はある――その程度に受け止めておけば良いぞい。
🌊 波高 × 払戻金
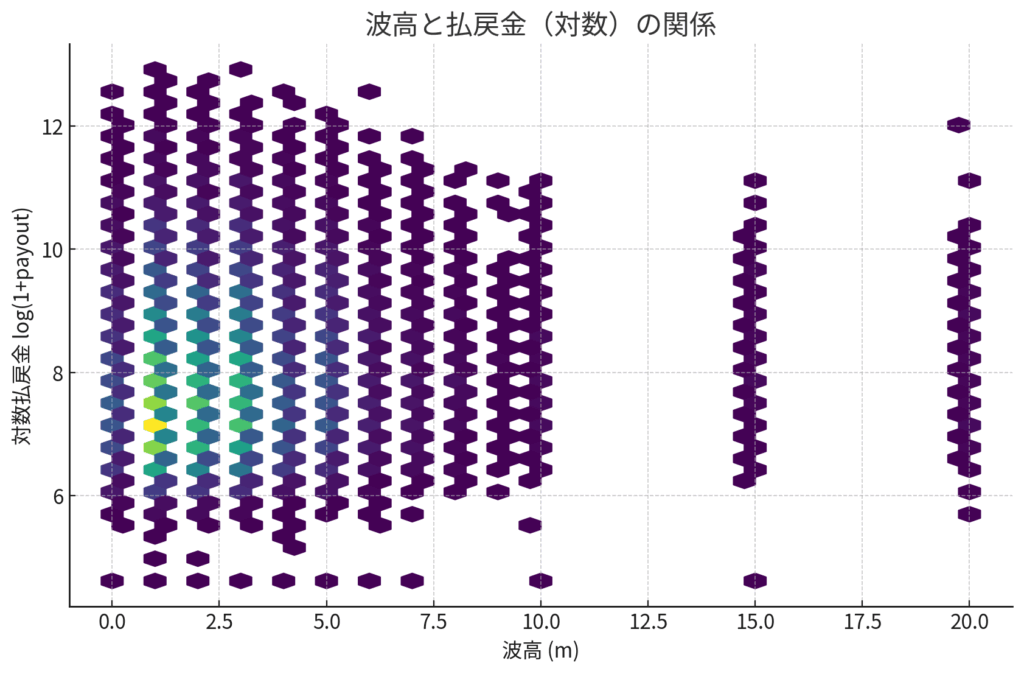
図の見方
- 横軸:波高(m)
- 縦軸:払戻金(自然対数)
- 目盛りの意味は風速の散布図と同じ(ln=6で約400円、ln=10で万舟券)
- 色:緑〜黄色=よく出るゾーン、紫=レアケース
分析
ほれ、この図も風速と同じじゃ。
緑や黄色の帯は波が低かろうが高かろうが 横にベターっと低配当域に広がる。
一方で、紫の点は波が低いときにも高いときにも上にポツポツ出ておる。
要するに、波が荒いから必ず万舟になる、という筋道は見えんのじゃ。
結論
波は舟券を揺らさない
波高と払戻金にも相関がないことが明らかになったのう。低波の日でも十万舟が出るし、高波でも安く収まることが多い。波が高いから「配当が荒れる」とは一概に言えん、これがデータの答えじゃ。
💨🌊 風速・波高 × イン逃げ失敗率
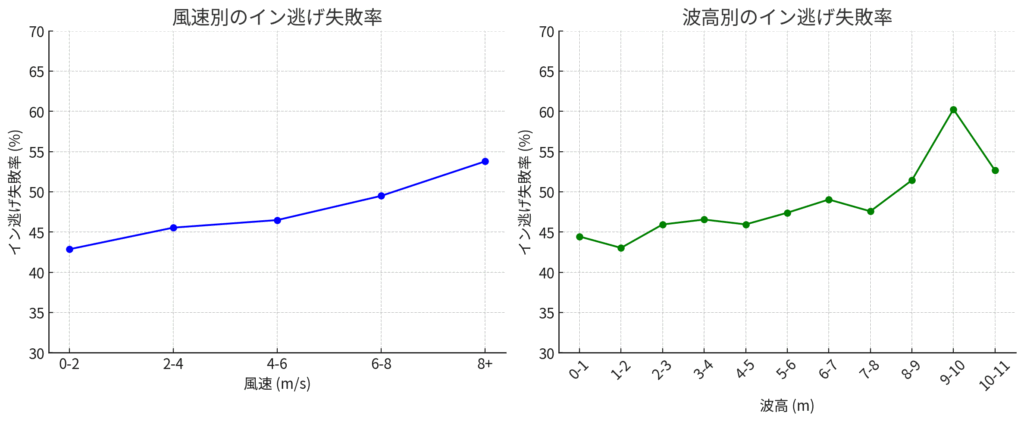
図の見方
- 横軸:風速または波高
- 縦軸:イン逃げ失敗率(%)
- 右上がりの線なら「条件が厳しいほどイン逃げが崩れる」ことを意味
分析
- 風速:弱風(2m/s未満)では失敗率は約43%。強風(8m/s以上)では50%超に上昇。線は全体として右上がり。
- 波高:1〜2mで43%前後。だが8mを超えると50%台、9〜10mでは60%以上に跳ね上がる。
結論
払戻金の大きさには直結しないが、戦略上「インの信頼度が落ちる」ことはハッキリ言えるんじゃ。風が強いほど、波が高いほどイン逃げは崩れやすいということじゃ。
🤔 まとめ
・風と波は舟券を揺らさない → 払戻金との相関はなし。万舟は凪の日にも、荒れた日にも等しく出る。
・イン逃げ失敗率との相関はあり → 強風・高波でインの信頼度が下がる。
ひっひっひ……
環境がすべて結果を決めるわけではない。
じゃが、環境は結果の「確率」をじわじわ動かすのじゃ。
人生も同じよ。追い風に乗れるときは思い切り漕ぎ出し、向かい風のときは身を低くしてしのぐ。
波風を味方にできる者こそ、勝負の荒海を渡り切れるんじゃぞい。
予想が聞ききたくなったらこっちにおいで~